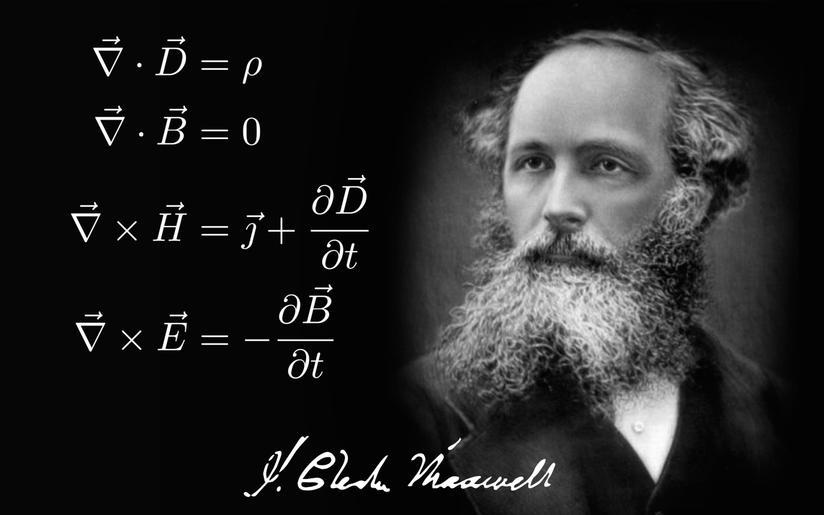
麦克斯韦方程组详解:从三个基础公式出发!—— Part2
上一节我们分析了库仑定律并且推导了麦克斯韦方程组的第一条方程,这是个不错的开头!让我们快马加鞭,在这一篇文章里,我们将推导出麦克斯韦方程组的第二和第三条方程!让我们快点开始吧!
第二条方程的直观解释
不知道大家有没有发现,世界上似乎不存在单极的“磁荷”?磁极似乎永远都有南北,就像一个物体永远都有正反一样。聪明的高斯深入思考了这个显然的规律,于是提出了个更加“显然”的公式!
想象一个简单的闭合曲面,因为正如刚刚所说,磁场永远都是闭合的!因此不存在什么地方会有“磁感线汇聚于一点”或“磁感线由这个源头向外发散”。于是,高斯说:任意一条磁场线,但凡它穿入这个闭合曲面,就一定会穿出去!用数学语言表述就是:
这就是麦克斯韦方程组的第二条方程!
法拉第电磁感应定律
其中 \Epsilon 为感应电动势, \Phi_B=\int_S\mathbf B\cdot\mathrm d\mathbf A 为磁通量,这里有人可能会问:为什么这里的 \int_S 不是上一节的闭合曲面积分 \oint_A ?这是因为上一节的电场高斯定律要求曲面包裹住点电荷,而这里没有这个连续曲面的要求!这里只需要磁场线穿过一个面即可,所以无需闭合曲面积分。
在开启下一步之前,我们要先搞明白电动势 \varepsilon 的定义,但因为主播喜欢用大写 \Epsilon ,这里大家就通融一下哈哈哈(别和标量场强 E 以及向量场强 \mathbf E 搞混了哦)。电动势 \Epsilon 本质上为单位电荷在电路中的移动提供了能量,换种说法就是单位电荷在电场中沿某条路径做功。而我们如何知道电动势的大小,也就是提供能量的“能力大小”呢?我们可以通过测量电动势在电路中对电荷施加的“压力”的总和来衡量。如果有一段的电场很强,“压力”就很大,反之亦然。我们把每一小段的“压力”都加起来,不就能得到电动势总的“供能能力”吗?
让我们规范一下刚刚的逻辑!我们现在知道了:电动势可以理解为沿闭合导线的电场积分,也就有了如下公式:
这里的 \mathbf E 是感应电场, C 是导线环路(所以这里的 \oint_C 是环路积分!)。
代入电磁感应公式:
三号方程完毕!
