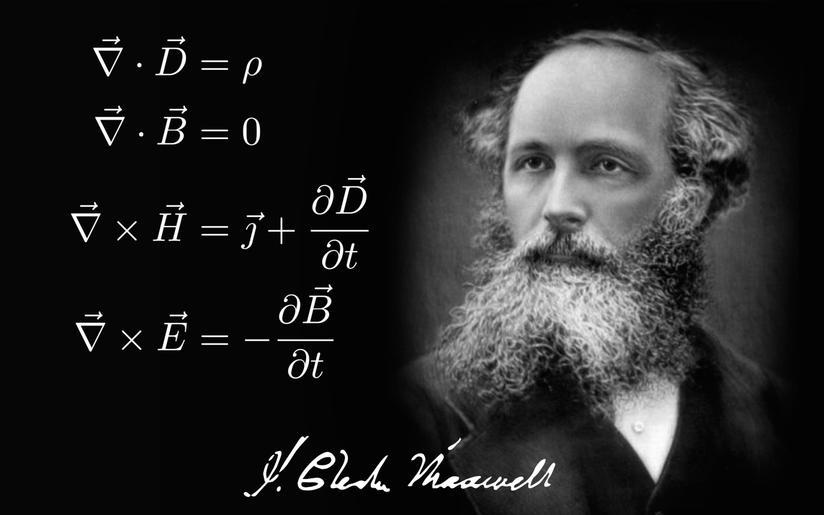
麦克斯韦方程组详解:从三个基础公式出发!—— Part1
回顾三个电磁学定律
我们中学学过三大公式,撑起整个中学的电磁学:库伦定律、安培定律、法拉第电磁感应定律。回顾一下,它们应该是:
也是非常的熟悉!那就让我们一个个仔细观察他们!
库仑定律
高中我们推导过:
其中 E 是场强, \hat{\mathbf r} 是一个方向向量,代表了场强的方向(例如,靠近一个正电荷,场强方向就是远离电荷的方向),中间的公式不必多说,就是场强的大小。
现在想象一块电场(是向量场),再想象一个小体积(例如正方体),电场就像水流一样流过这块体积。我们定义一个“流量”,也就是这块体积有多少水汇入,多少水输出。它们的差就是“流量”,也就是我们的电场通量 \Phi_E 。我们继续定义字母 A 为包裹体积的表面。
聪明的你肯定发现了:把整块表面积化为一块块极小的 \Delta A ,计算电场 E 在每块小表面上的通量,再全部加起来,不就得到了整块体积的电场通量了嘛!于是你提出:
这里, \mathrm d\mathbf A 的大小就是一块微小的面积,它的方向指向体积的外部。这么做的原因是因为流入定义为负,流出定义为正(如果你想反过来定义, \mathrm d\mathbf A 就应该是朝内的了哈哈)。这里的 \mathbf E \cdot \mathrm d\mathbf A 可以拆解为 \left(\mathbf E_{||}+\mathbf E_{\perp}\right)\cdot\mathrm d\mathbf A ,也就是这个点的场强可以分解为平行和垂直 \mathrm d\mathbf A 的分量。而你也发现该式的后半段直接等于 0 !于是“斜向流入”也就自动变成了“垂直流入”,这下一点歧义也没有了!当然但凡有点基础都知道点乘就是只保留投影的哈哈但是我就是要重申一遍。另外,这个吓人的积分号 \oint_A 作用就是求和,但它额外声明了一下表面 A 一定是一个闭合曲面,因为破洞的表面我们无法计算通量(注意这个符号是闭合曲面积分而不是环路积分啊啊!)。
我们让这块体积包裹一个点电荷,会发现无论包裹电荷的表面形状怎么变,穿出表面的电场线的数量一定保持一致!就好比用一个篮子打水,无论篮子长什么样,水流出篮子缝隙的量永远是固定的。那如果把点电荷放在一个包裹电荷的球体的球心,就不难发现每条场线恰好都垂直通出球面,直接无需点乘“取投影”的操作,大大简化计算!于是我们理所应当的代入球面 A=4\pi r^2 与公式 (1) ,推出:
其中 \varepsilon_0=1/4k\pi 。
细心的你一定观察到了:主播主播,为什么刚刚那一段你用了粗体的 \mathbf E 而这里推导你却没加粗 E ?这里不是主播失误,而是刚刚的 \mathbf E 是在某点的向量,现在的 E 已经不需要向量形式了(刚刚已经提到,点乘被球体简化了),所有球体表面上的场强都相同,都是 E !
于是,麦克斯韦方程组一号公式闪亮登场,无论什么样的表面,只要包裹一个相同的点电荷,电场通量都相同!这就是电场高斯定律:
